Da wird sich doch der eine oder andere fragen, was diese seltsame Überschrift zu bedeuten hat. *gg* Also heute in diesem Kino nicht etwa das Wasserlassen von Kleinkindern sondern:
Wie transformiere ich Winkel in das Intervall [−π, π]?
Das Problem stellte sich mir vor einigen Wochen im Rahmen meiner Studienarbeit das erste mal. Ich hatte zunächst einen Algorithmus entwickelt, der sich in einer Schleife so lange dem Zielintervall näherte, bis der Winkel transformiert war. Das ist zuverlässig, leicht zu durchschauen und langweilig. Meine Idee für eine elegante einzeilige Lösung war ein wenig mit der Signum-Funktion rumzuspielen und durch geschicktes Anwenden von Runden und aller vier Grundrechenarten die Geschichte mit der Schleife zu umgehen.
Im Prinzip gehe ich dabei ähnlich vor wie im Schleifenalgorithmus: ich addiere oder subtrahiere solange Vielfache von 2π bis ich im Zielintervall bin. Will ich das in einer Zeile tun, muss ich das notwendige Vielfache rausbekommen und das Vorzeichen.
Stellt man sich den allseits beliebten Zahlenstrahl vor – vorstellen mit Zettel und Stift ist leichter ;-) – erkennt man die Zuordnung:
- [−5π, −3π] : 2
- [−3π, −π] : 1
- [−π, π] : 0
- [π, 3π] : −1
- [3π, 5π] : −2
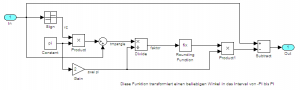
Das Intervall [−π, π] um 0 rum stört. Das erste was ich deshalb tue: ich addiere sign(inAngle)*π zu meinem Einganswinkel inAngel. Dadurch schaffe ich mir zwar einen toten Bereich um 0 rum, aber die neuen Abschnitte haben ihre Grenzen bei vollen Vielfachen von 2π, so dass ich nun durch 2π teilen kann. Das Ergebnis runde ich derart, dass ich auf die nächste volle Zahl in Richtung 0 runde, d.h. ich runde bei positiven Zahlen ab und bei negativen auf oder kurz gesagt: ich schneide einfach die Nachkommastellen des Divisionsergebnisses ab. ;-) Damit habe ich schon die gesuchten Koeffizienten mit richtigem Vorzeichen. Die multipliziere ich dann wieder mit 2π und das Ergebnis ziehe ich vom Eingangswinkel ab, fertig. In Simulink sieht das dann aus wie auf dem folgenden Bild (zum Vergrößern anklicken):
In Matlab liest sich das wie folgt:
function outAngle = MinusPiPiTransform(inAngle)
outAngle = inAngle - ...
fix( (inAngle + sign(inAngle)*pi) / (2*pi) ) * ...
2*pi;
end%function
Diese Lösung hatte ich wie gesagt vor ein paar Wochen entwickelt. Heute brauchte ich das ganze wieder, allerdings in C# – kein Problem. Einfach den Teil aus dem Matlab-Skript in C# übersetzt und dann sieht das ganze so aus:
public double MinusPiPiTransform(double inAngle) {
return inAngle -
Math.Truncate((inAngle + Math.Sign(inAngle) * Math.PI) / (2 * Math.PI)) *
2 * Math.PI;
}
Wenn man in Grad statt Radiant rechnet, kann man das ganze dank Modulo-Operator einleuchtender schreiben:
degrees = degrees % 360; if (degrees >= 180) { degrees = 180 - degrees; }In C# und Matlab funktioniert der Modulo-Operator auch mit Gleitkomma-Zahlen, allerdings erwähnt die Matlab-Hilfe dazu, dass dies numerische Probleme hervorrufen kann. Andere Sprachen kennen den Operator aber nur für Ganzzahlen.