Vor einiger Zeit hatte ich im Beitrag Schicke Grafiken aus Matlab in LaTeX Möglichkeiten ausgelotet aus mit Matlab erzeugten Daten schicke Plots in LaTeX zu generieren. Sehr vielversprechend war dort das Paket pgfplots bei dem sich in den letzten Monaten einiges getan hat. Es liegt mittlerweile in Version 1.1 vor und hat neben dem Einbinden externer Datenquellen noch so manches dazugelernt. Ich möchte in diesem und einem folgenden Artikel an zwei Beispielen zeigen, wie man mit pgfplots tolle Ergebnisse produzieren kann.

Zunächst bleiben wir bei Matlab. Aus Matlab heraus ist es vergleichsweise einfach das .table-Format zu erzeugen, aus dem pgfplots Werte einlesen kann. Im einfachsten Fall benutzt man die Funktion dlmwrite. Will man auch noch Header und Kommentarzeilen in das Zwischenformat packen, muss man bisschen mehr Aufwand betreiben, ein entsprechendes Skript ist aber in kurzer Zeit fertiggestellt und bleibt dem geneigten Leser als Hausaufgabe überlassen. ;-) Meine Datei dahl_2008-08-19_05.table beginnt jedenfalls wie folgt:

time datadownsampled datadecimated dataresampled impactdownsampled impactdecimated impactresampled
7.2 0.0042314 0.0031181 0.0017701 7.6889e-005 7.5995e-005 4.3056e-005
7.201 0.010326 0.0048359 0.0049109 8.081e-005 8.0715e-005 8.7923e-005
7.202 0.013369 -0.0069568 -0.006471 7.9993e-005 8.087e-005 7.8394e-005
7.203 -0.011055 -0.010981 -0.011697 6.9248e-005 7.0035e-005 7.2734e-005

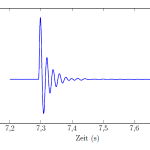
Es folgen knapp fünfhundert weitere Zeilen. Wie man bereits am Header sieht ist es empfehlenswert ein Downsampling der zu plottenden Daten vorzusehen, wenn eine Datenreihe mehr als ein paar hundert Elemente enthält. Diese spezielle Datei enthält in der ersten Spalte die Zeit, in den Spalten zwei bis vier ein Signal und in den Spalten fünf bis sieben ein zweites Signal. Für beide Signale wurden je drei verschiedene Downsampling-Verfahren ausgetestet, das jedoch nur nebenbei und zur Erläuterung, für den Plot werde ich nur die Spalten time und datadownsampled nutzen.

In LaTeX-Dokument sollten die notwendigen Pakete geladen sein, in diesem Fall sieht das bei mir so aus:

usepackage{tikz}
usepackage{pgfplots}
pgfplotsset{every axis plot/.append style={very thick}}

Die Einbindung selbst erfolgt wie gewohnt in einer float-Umgebung, die das ganze zentriert und auch noch label und Bildunterschrift bereit stellt. Statt includegraphics fügt man aber einfach eine tikzpicture-Umgebung ein:

begin{figure}[htb]
	centering
	begin{tikzpicture}
		begin{axis}[
			xlabel=Zeit (s),
			ylabel=Kraft (N),
			width=12cm,
			height=8cm]
		addplot[smooth,color=blue]
			table[x=time,y=datadownsampled] {plots/dahl_2008-08-19_05.table};
		end{axis}
	end{tikzpicture}
	caption{Rohdaten Messung texttt{dahl_2008-08-19_05}}
	label{fig:rohdaten_dahl_2008-08-19_05.txt}
end{figure}

Wichtig für das Lesen aus der externen .table-Datei ist die Anweisung table in der Zeile beginnend mit addplot. Das Ergebnis ist eine Vektorgrafik. Die Achsen sind wunderbar mit der im restlichen LaTeX-Dokument verwendeten Schrift beschriftet und zwar immer in der richtigen Größe. Mit extern als .eps oder ähnlichen Formaten eingebundenen Grafiken ist so etwas kaum möglich. Das Ergebnis spricht für sich:

Ich arbeite mit LaTeX und ich arbeite mit Matlab. Bei meiner letzten Arbeit habe ich die Grafiken in Matlab einfach als .eps-Datei exportiert und unverändert in meine TeX-Dateien eingebunden. Das funktioniert problemlos, sieht aber nicht so schick aus, wie es könnte. Da ich für andere Grafiken das wunderbare Paket PGF und TikZ von Till Tantau benutze, habe ich heute Möglichkeiten ausgelotet wie man mit PGF Matlab-Grafiken schick machen könnte. Gründe dafür werden in der Doku von PGF genügend angeführt:

However, there are a number of reasons why you may wish to invest time and energy into mastering the PGF commands for creating plots:

• Virtually all plots produced by »external programs« use different fonts from the one used in your document.
• Even worse, formulas will look totally different, if they can be rendered at all.
• Line width will usually be too large or too small.
• Scaling effects upon inclusion can create a mismatch between sizes in the plot and sizes in the text.
• The automatic grid generated by most programs is mostly distracting.
• The automatic ticks generated by most programs are cryptic numerics. (Try adding a tick reading »π« at the right point.)
• Most programs make it very easy to create »chart junk« in a most convenient fashion. All show, no content.
• Arrows and plot marks will almost never match the arrows used in the rest of the document.

The above list is not exhaustive, unfortunately.

Neben PGF selbst gibt es das Paket pgfplots von Christian Feuersänger, das es leicht macht, einheitliche Plots zu erstellen und sogar logarithmische oder semi-logarithmische Achsen ermöglicht. Leider scheint man bei pgfplots im Gegensatz zu PGF selbst noch keine externen Dateien mit den zu plottenden Werten einbinden zu können. Das Skript matlab2pgfplots.m funktioniert leider nicht mit dem steinalten Matlab 6.1 hier im Institut, also habe ich noch nach weiteren Möglichkeiten gesucht.

Paul Wagenaar hat zwei interessante Tools geschrieben. Mathfig2pgf ist ebenfalls ein Matlab-Skript zur Umwandlung in PGF, funktioniert aber leider auch nicht mit Matlab 6.1. Das zweite Tool ist Eps2pgf und erinnert nicht von ungefähr an PSfrag. Beispiele für Ergebnisse von eps2pgf kann man sich auf fauskes.net ansehen.

Da ich nicht nur ein paar wenige Werte zu plotten habe, bin ich mir noch nicht sicher, welche Variante ich wählen werde. In Frage kommt außerdem noch die LowLevel-Variante mit PGF allein. Ein Beispiel wie man dort externe Datenquellen, z.B. den Output von gnuplot einbindet ist dokumentiert, allerdings muss man sich dann wieder Achsen etc. alles selbst bauen, also wird es wahrscheinlich die Variante mit eps2pgf werden, es sei denn pgfplots wird um die Funktion zur Nutzung externer Datenquellen erweitert. Kommt Zeit, kommt Rat, so dringend ist das Problem ja nicht.